▷ 前を見る　

11.1-9　三角形（triangle）

三角形をいくつも組み合わせることで、他のプリミティブではできない複雑な形状を作ることができる。メッシュ（mesh）の要素としても使用できる。

図11.1-9　三角形（triangle）
//--------------- Fig. 11.1-9 /triangle/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<2,-2,0.6> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,-0.3,0.6> } light_source {<300,-1000,1000> color White} //================================ /// triangle /// triangle{<-1,-1,0>,<1,-1,0>,<0,1.23,0> pigment{checker White*1.2, color rgb<1,0.3,0.3> scale 0.5} finish{phong 1 reflection 0.2} rotate <30,30,0> translate z*1 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.05} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.3 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限パッチ
　　●クリッピング形状：×
　　●CSG：△（曲面の端部は×）

＜ triangle の構文 ＞

triangle { <CORNER1>, <CORNER2>, <CORNER3> [ OBJECT_MODIFIERS... ] }
triangle ３角形のキーワード
<CORNER1>
～ <CORNER3>		 ３角形の各頂点の x,y,z 座標
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

11.1-10　スムーズ３角形（smooth_triangle）

スムーズ３角形は、３角形の各頂点の法線ベクトルを修正し、３角形のつなぎ目を滑らかに見せる。

スムーズ３角形（左側）、３角形による物体（右側）
図11.1-10a　スムーズ３角形（smooth_triangle）

上図の２つの図形は同じ４角錐の形状である。左側で使ったスムーズ３角形は、下図 11.1-10b に示すような頂点の法線ベクトルを使用している。（右側は通常の３角形による図形）

//--------------- Fig. 11.1-10a /smooth_triangle/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-2,4> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0> angle 38 } light_source {<300,-100,600> color White} //================== /// smooth_triangle /// #declare vec1 = <-0.41,-0.41,0.82>; #declare vec2 = < 0.41,-0.41,0.82>; #declare vec3 = < 0.41, 0.41,0.82>; #declare vec4 = <-0.41, 0.41,0.82>; #declare vecz = <0,0,1>; union{ smooth_triangle{ <-1,-1,0>, vec1 <1,-1,0>, vec2 <0,0,1>, vecz } smooth_triangle{ <1,-1,0>,vec2 <1,1,0>,vec3 <0,0,1>,vecz } smooth_triangle{ <1,1,0>,vec3 <-1,1,0>,vec4 <0,0,1>,vecz } smooth_triangle{ <-1,1,0>,vec4 <-1,-1,0>,vec1 <0,0,1>,vecz } pigment{color White} finish{phong 1 reflection 0.2} translate x*-1.1 scale 0.5 } //======================= triangle union{ triangle{<-1,-1,0>,<1,-1,0>,<0,0,1>} triangle{<1,-1,0>,<1,1,0>,<0,0,1>} triangle{<1,1,0>,<-1,1,0>,<0,0,1>} triangle{<-1,1,0>,<-1,-1,0>,<0,0,1>} pigment{color White} finish{phong 1 reflection 0.2} translate x*1.1 scale 0.5 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.1} normal{brick 0.01 scale 0.1} // finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限パッチ
　　●クリッピング形状：×
　　●CSG：△（曲面の端部は×）

＜ smooth_triangle の構文 ＞

smooth_triangle { <CORNER1>, <NORMAL1>, <CORNER2>, <NORMAL2>, <CORNER3>, <NORMAL3> [ OBJECT_MODIFIERS... ] }
smooth_triangle スムーズ３角形のキーワード
<CORNER1>～<CORNER3> ３角形の各頂点の x,y,z 座標
<NORMAL1>～<NORMEL3> 各頂点における面の法線ベクトル
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

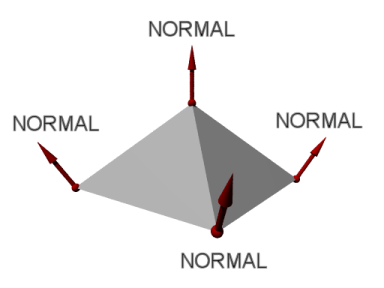※ 法線ベクトルの修正によってつなぎ目が滑らかに見えるのは見かけ上のものであって、 実際に平面が曲面になっているわけではない。

各頂点の法線ベクトルが、その頂点を共有するすべての３角形の法線ベクトルの平均になれば滑らかな表面が得られる。

図11.1-10b　頂点の法線ベクトル

11.1-11　多角形（polygon）

多角形は同一平面上で３個以上の頂点を設定して作る。１つのステートメントの中で複数の多角形を作ることができる。また、偶数個の図形が重なった部分は穴になる。

図11.1-11　多角形（polygon）

上図の一番右側の三角形が６つある図形は、左側にある三角形２つを重ね合わせている。重なりあった部分がなくなり、このような図形が生成されている。

//--------------- Fig. 11.1-11 /polygon/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-3,4> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,1> } light_source {<300,500,10000> color White} //============================= /// polygon /// union{ polygon{ //----( triangle 1 ) 4, <-0.5,-0.5>,<0.5,-0.5>,<0,1.23>,<-0.5,-0.5> translate x*-2 } polygon{ //----( + ) 13, <-0.2,0.05>,<-0.05,0.05>,<-0.05,0.2>,<0.05,0.2>, <0.05,0.05>,<0.2,0.05>,<0.2,-0.05>,<0.05,-0.05>, <0.05,-0.2>,<-0.05,-0.2>,<-0.05,-0.05>,<-0.2,-0.05>, <-0.2,0.05> translate x*-1 } polygon{ //----( triangle 2 ) 4, <-0.5,0.5>,<0.5,0.5>,<0,-1.23>,<-0.5,0.5> } polygon{ //----( = ) 10, <-0.2,0.15>,<0.2,0.15>,<0.2,0.05>,<-0.2,0.05>,<-0.2,0.15>, <-0.2,-0.15>,<0.2,-0.15>,<0.2,-0.05>,<-0.2,-0.05>,<-0.2,-0.15> translate x*1 } polygon{ 8, <-0.5,-0.5>,<0.5,-0.5>,<0,1.23>,<-0.5,-0.5>, //---triangle 1 <-0.5,0.5>,<0.5,0.5>,<0,-1.23>,<-0.5,0.5> //---triangle 2 translate x*2 } pigment{color rgb<0.8,1,0.95>*1.5} // pigment{color rgb<0.8,1,0.7>*1.5} finish{reflection 0.1 } rotate x*30 translate z*1 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.1} normal{brick 0.01 scale 0.4} finish{reflection 0.2 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限パッチ
　　●クリッピング形状：×
　　●CSG：△（曲面の端部は×）

＜ polygon の構文 ＞

polygon { TOTAL_NUMBER_OF_POINTS, <A_1>, <A_2>, ..., <A_na>, <A_1>, <B_1>, <B_2>, ..., <B_nb>, <B_1>, <C_1>, <C_2>, ..., <C_nc>, <C_1>, ... [ OBJECT_MODIFIERS... ] }
polygon 多角形のキーワード
TOTAL_NUMBER_OF_POINTS 多角形を描く点の総数
<A_1>, ..., <A_na>, <A_1>,
<B_1>, ..., <B_nb>, <B_1>,
<C_1>, ..., <C_nc>, <C_1>,
...		 多角形の各頂点の x,y,z 座標
<A_1>,...、<B_1>, ... 、<C_1>, ... はそれぞれ別の要素図形を描く。
各図形は最初と最後の点を一致させて閉じなければならない。各点は同一平面上に設定しなければならない。２次元ベクトルで設定した場合は x-y 平面上に描かれる。偶数個の図形が重なった部分は穴になる。
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

11.1-12　メッシュ（mesh）

メッシュは、たくさんの３角形を合わせて複雑な形状をつくるためのものである。メッシュで使用する３角形は個別にテクスチャを付けることができるので、面ごとに異なったテクスチャを持つ物体をつくることができる。また、CSGにおけるunion（論理和）に比べてメモリの消費が少なく、多くの３角形を効率的に蓄積できる。モデリングソフトで作った複雑な曲面を表現するために使われることもある。

図11.1-12　メッシュ（mesh）
//--------------- Fig. 11.1-12 /mesh/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<1,-2,2> sky<0,0,1> right<-1.33,0,0> look_at<0,0,0.5> } light_source {<-300,-500,500> color White*1.5} /////////////////////////////////////////// texture #declare T_1= texture{ pigment{checker MediumTurquoise, Orange scale 0.1} finish{phong 1 reflection 0.2} } #declare T_2= texture{ pigment{brick White, MediumSpringGreen scale 0.05} finish{phong 1 reflection 0.2} } #declare T_3= texture{ pigment{ onion color_map{ [0.0 NeonPink*1.2] [1.0 White*0.0] } scale 0.1 } finish{phong 1 reflection 0.2} } #declare T_4= texture{ pigment{ quilted color_map{ [0.0 Light_Purple] [1.0 Black] } scale 0.1 } finish{phong 1 reflection 0.2} } #declare Tri= mesh{ triangle{x,y,z texture{T_2}} triangle{y,-x,z texture{T_3}} triangle{-x,-y,z texture{T_1}} triangle{-y,x,z texture{T_4}} scale z*0.5 rotate x*30 translate z*0.5 } object{Tri} //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.1} normal{brick 0.01 scale 0.4} finish{reflection 0.2 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限パッチ
　　●クリッピング形状：×
　　●CSG：△（面の端部は×）

＜ mesh の構文 ＞

mesh { triangle{ ITEM_V [uv_vectors ITEM_UV] [texture { TEXTURE_IDENTIFIER } ] } | smooth_triangle{ ITEM_VN [uv_vectors ITEM_UV] [texture { TEXTURE_IDENTIFIER } ] } [ inside_vector <direction> ] [ hierarchy on|off ] [ OBJECT_MODIFIER... ] } ここで ITEM_V : <Corner_1>, <Corner_2>, <Corner_3> ITEM_UV : <uv_Corner_1>, <uv_Corner_2>, <uv_Corner_3> ITEM_VN: <Corner_1>, <Normal_1>, <Corner_2>, <Normal_2>, <Corner_3>, <Normal_3>
mesh メッシュのキーワード
triangle ３角形の設定　 ▷「11.1-8 ３角形」参照
smooth_triangle スムーズ・トライアングルの設定　▷「11.1-9 スムーズ３角形」参照
uv_vectors UVマッピング用の２次元ベクトルの設定
texture テクスチャの設定
inside_vector CSG論理演算における内外判定用ベクトルの設定
hierarchy 階層バウンディングをon/offにするスイッチ、[ディフォルト：on ］
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

11.1-13　メッシュ２（mesh2)

メッシュ２はメッシュと同様なものであるが、さらにPOV-Rayの内部表現に近いものである。メッシュより実行速度も速くサイズも小さいが、メッシュ２のデータ作成は手作業には向いていない。他のモデラーなどで作成したデータを変換し、メッシュ２で使用するようなことに向いている。

図11.1-13　メッシュ２（mesh2)
//--------------- Fig. 11.1-13 /mesh2/ #version 3.7 #include "colors.inc" #include "stones.inc" global_settings {assumed_gamma 2.2} camera{ location<5,10,10> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0.5,0.5,0> angle 7 } light_source { <300,500,500> color 2 parallel point_at <0,0,0>} //========================== /// mesh2 /// mesh2 { vertex_vectors { 9, <0,0,0>, <0.5,-0.2,0>, <0.5,0.5,0.3>, <1,0,0>, <1.2,0.5,0>, <1,1,0>, <0.5,1.2,0>, <0,1,0>, <-0.2,0.5,0> } face_indices { 8, <0,1,2>, <1,3,2>, <3,4,2>, <4,5,2>, <5,6,2>, <6,7,2>, <7,8,2>, <8,0,2> } texture {T_Stone3} } //----------------ground disc{z*-3, <0,0,1>, 5 pigment{brick White, CoolCopper*0.8 scale 0.05} normal{brick 0.01 scale 0.1} // finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限パッチ
　　●クリッピング形状：×
　　●CSG：△（面の端部は×）

＜ mesh2 の構文 ＞

mesh2{ vertex_vectors { ITEM_VERTEX } [ normal_vectors { ITEM_NORMAL_V } ] [ uv_vectors { ITEM_UV_V } ] [ texture_list { ITEM_TLIST } ] face_indices { ITEM_FACE } [ normal_indices { ITEM_NORMAL_I } ] [ uv_indices { ITEM_UV_I } ] [ inside_vector <direction> ] [ OBJECT_MODIFIERS... ] } ここで ITEM_VERTEX：Number_of_Vertices, <vertex1>, <vertex2>, ... ITEM_NORMAL_V：Number_of_Normals, <normal1>, <normal2>, ... TEM_UV_V：Number_of_Uv_vectors, <uv_vect1>, <uv_vect2>, ... ITEM_TLIST：Number_of_Textures, texture { Texture1 }, texture { Texture2 }, ... } ITEM_FACE：Number_of_Faces, <index_a, index_b, index_c> [,Texture_index [, Texture_index, Texture_index]], <index_d, index_e, index_f> [,Texture_index [, Texture_index, Texture_index]], ... ITEM_NORMAL_I：Number_of_Faces, <index_a, index_b, index_c>, <index_d, index_e, index_f>, ... ITEM_UV_I：Number_of_Faces, <index_a, index_b, index_c>, <index_d, index_e, index_f>, ...
mesh2 メッシュ２のキーワード
vertex_vectors ３角形の頂点となる各点の設定
normal_vectors 各点の法線ベクトルの設定
uv_vectors 各点のUVマッピング用の２次元ベクトルの設定
texture_list テクスチャ リストの設定
face_indices 各点の番号で各３角形を設定
normal_indices 各点の番号でスムージングする各３角形を設定
uv_indices 各ベクトル番号で各３角形のUVマッピング用ベクトルの設定
inside_vector <direction> CSG論理演算における内外判定用ベクトルの設定
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

11.1-14　簡易回転体（sor）

簡易回転体は、x-y 平面上の２次元曲線をy軸まわりで回転させた軌跡によって形成される立体である。設定した x-y 平面上の２次元座標座標が３次スプラインで補間され、曲線が作られる。この曲線を y 軸回りに回転し、立体を生成する。

図11.1-14　簡易回転体（sor）
//----------------------- Fig. 11.1-14 /sor/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-3,3> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,1.2> } light_source {<-300,-1000,1000> color White} //======================================= /// sor /// sor{ 13, <0,0>,<0.5,0.01>,<0.5,0.1>,<0.4,0.11>,<0.4,0.2>, <0.3,0.21>,<0.3,1.89>,<0.4,1.9>,<0.4,1.99> <0,2>,<0.3,2.2>,<0,2.4>,<0,2.5> sturm pigment{Copper*1.5} finish{reflection 0.3} rotate x*90 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ sor の構文 ＞

sor { NUMBER_OF_POINTS, <POINT_0>, <POINT_1>, ..., <POINT_n-1> [ open ] [ sturm ] [ OBJECT_MODIFIERS... ] }
sor 回転体のキーワード
NUMBER_OF_POINTS 曲線を描く点の数を設定
<POINT_0>
～ <POINT_n-1>		 曲線を描く各点の x,y 座標の設定をする。x は回転の半径、y は高さとなる。元になる曲線は、３次スプラインで描かれる。最初の点と最後の点は、曲線の始まりと終わりの傾きの制御点となる。ある高さに２つ以上の半径を設定はできない。つまり、y座標の値は常に増加しなければならない。スプライン曲線：▷「11.1-14 回転体：スプライン曲線について」参照
open 回転体の両端面を取り除く設定、openを使用した回転体はCSGでは適切に描かれない場合がある。
sturm 形状が正しく描かれない場合に、時間をかけて正確に計算をする設定
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

※ 次の回転体（lathe）ほど複雑な形状は扱えないが、簡単な形状であればこちらのほうがレンダリングが速い。

11.1-15　回転体（lathe）

回転体は x-y 平面上の２次元曲線を y 軸まわりに回転させた軌跡によって生成される立体である。この曲線は設定した x-y 平面上の２次元座標座標が補間され作られる。曲線補間には１次～３次のスプライン曲線が使われ、２次と３次のスプラインでは曲線の傾きを制御できる。この曲線を y 軸回りに回転し、立体を生成する。

左から １次、２次、３次スプラインを使用
図11.1-15a　回転体（lathe）
//--------------------- Fig. 11.1-15a /lathe/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-3.5,3> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,1.2> } light_source {<300,-1000,1000> color White} //==================left-========= /// lath (linear_spline) /// lathe{ linear_spline 10, <1,0>,<1,0.1>,<0.5,0.4>,<1,1.5>,<0.5,2>, <0.4,2>,<0.9,1.5>,<0.4,0.4>,<0.8,0>,<1,0> pigment{color rgb<1,0.7,0.4>} finish{phong 1 reflection 0.1} rotate x*90 scale<0.5,0.5,1> translate x*-1.5 } //==================center==== /// lath (quadratic_spline) /// lathe{ quadratic_spline 11, <1,0>,<1,0.1>,<0.5,0.4>,<1,1.5>,<0.5,2>, <0.4,2>,<0.9,1.5>,<0.4,0.4>,<0.8,0>,<1,0>,<1,0.1> pigment{color rgb<0.7,1,0.4>} finish{phong 1 reflection 0.1} rotate x*90 scale<0.5,0.5,1> sturm } //==================right========= /// lath (cubic_spline) /// lathe{ cubic_spline 12, <1,0>,<1,0.1>,<0.5,0.4>,<1,1.5>,<0.5,2>, <0.4,2>,<0.9,1.5>,<0.4,0.4>,<0.8,0>,<1,0>,<1,0.1>,<0.5,0.4> pigment{color rgb<0.4,0.7,1>} finish{phong 1 reflection 0.1} rotate x*90 scale<0.5,0.5,1> translate x*1.5 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ lathe の構文 ＞

lathe { [ linear_spline | quadratic_spline | cubic_spline | bezier_spline ] NUMBER_OF_POINTS, <P_1>, <P_2>, ..., <P_n> [ sturm ] [ OBJECT_MODIFIERS... ] }
lathe 回転体のキーワード
linear_spline １次スプラインの設定、すべての点が直線で結ばれる。
quadratic_spline ２次スプラインの設定、曲線の始まりの傾きを制御できる。
cubic_spline ３次スプラインの設定、曲線の始まりと終わりの傾きを制御できる。
bezier_spline bezierスプラインの設定
NUMBER_OF_POINTS 曲線を形成する点の個数
<P_1> ～ <P_n> 曲線を形成する各点の x,y 座標
sturm 形状が正しく描かれない場合に、時間をかけて計算を正確にする設定（２次スプラインのみ）
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

※ デフォルトではlinear_splineが使用される。

※ 曲線は自動的には閉じられない。

スプライン曲線について

●１次スプライン

１次スプラインは単に各点を直線でつなぐだけのものである。平面をつくる場合は最初の点と最後の点を一致させなければならない。つまり、

<P_n> = <P_1>

としなければならない。

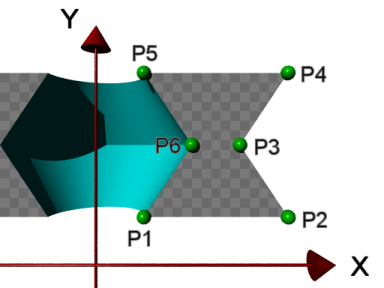図11.1-15b　１次スプライン

●２次スプライン

２次スプラインは曲線の始まりの傾きを制御できる。例えば点P2から点P3までの曲線の始まりの傾きはP1，P2，P3の位置関係によって決まる。ただし、曲線の終わりの部分の傾きは制御できないため、各点でのつなぎ目は滑らかにならない。２次スプラインでは最初に設定した点は傾きの制御点となるため、平面をつくる場合は、次のようにすべきである。

<P_n-1> = <P_1>（曲線を閉じる）

<P_n> = <P_2>（滑らかにつなぐ）

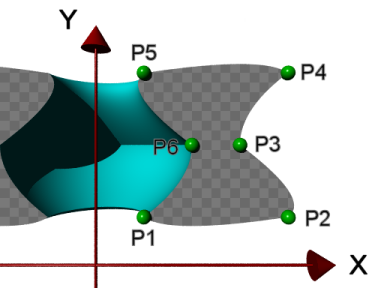図11.1-15c　２次スプライン

●３次スプライン

３次スプラインは曲線の始まりと終わりの傾きを制御できる。ある点Pnにおける曲線の傾きはP(n-1)、Pn、P(n+1)の位置関係によって決まる。２次スプラインと違って各点の両側の傾きが制御できるため、曲線は滑らかにつながれる。３次スプラインでは最初と最後に設定した点は傾きの制御点となるため、平面をつくる場合は、次のようにすべきである。

<P_n-1> = <P_2>（曲線を閉じる）

<P_n> = <P_3>、 <P_n-2> = <P_1>（滑らかにつなぐ）

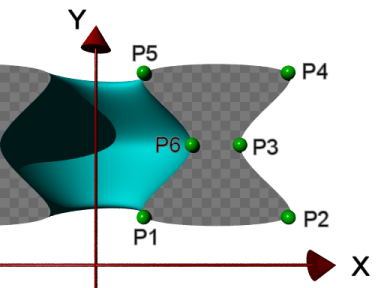図11.1-15d　３次スプライン

11.1-16　角柱（prism）

角柱は２次元図形をスイープ（ここでは平行移動）し生成する。このような図形は一般には押し出し図形とかスイープ図形といわれている。２次元図形は x-z 平面に作成し、y 軸に沿ってスイープが行われる。角柱の断面である２次元図形は、スプライン補間が使えるため、曲面の柱を作ることもできる。

次の図11.1-16a 角柱は、三角形、四角形、五角形をスイープし作成した。前列は２次元図形そのままのスイープ、後列は２次元図形を２次スプライン補間し、曲面にしている。

図11.1-16a　角柱（prism）
//--------------- Fig. 11.1-16a /prism/ #version 3.7 #include "colors.inc" #include "textures.inc" #include "stones.inc" global_settings {assumed_gamma 2.2} camera{ location<5,-20,10> sky<0,0,1> right <-image_width/image_height,0,0> look_at<-0.3,0,1.3> angle 25 } light_source {<500,-500,1000> color White*1.5} //====================== define /// sweep triangle /// #declare prism_1a= prism{ linear_sweep linear_spline 0,3.5, 4, <0,0>,<1.5,0>,<0.75,1.3>,<0,0> } #declare prism_1b= prism{ linear_sweep quadratic_spline 0,3.5, 5, <0,0>,<1.5,0>,<0.75,1.3>,<0,0>,<1.5,0> } //====================== define /// sweep rectangle /// #declare prism_2a= prism{ linear_sweep linear_spline 0,3.5, 5, <0,0>,<1.5,0>,<1.5,1>,<0,1>,<0,0> } #declare prism_2b= prism{ linear_sweep quadratic_spline 0,3.5, 6, <0,0>,<1.5,0>,<1.5,1>,<0,1>,<0,0>,<1.5,0> } //====================== define /// sweep pentagon /// #declare prism_3a= prism{ linear_sweep linear_spline 0,3.5, 6,<0.2,0>,<1.3,0>,<1.5,0.8><0.7,1.3>,<0,0.8>,<0.2,0> } #declare prism_3b= prism{ linear_sweep quadratic_spline 0,3.5, 7,<0.2,0>,<1.3,0>,<1.5,0.8><0.7,1.3>,<0,0.8>, <0.2,0>,<1.3,0> } //============================== place Object 1 union{ object{prism_1a rotate x*90 translate<-3.5,-2,0>} object{prism_2a rotate x*90 translate<-1,-2,0>} object{prism_3a rotate x*90 translate<1.3,-2,0>} texture {T_Grnt29 scale 0.5} finish{phong 1 reflection 0.2} } //============================== place Object 2 union{ object{prism_1b rotate x*90 translate<-3.5,2,0>} object{prism_2b rotate x*90 translate<-1,2,0>} object{prism_3b rotate x*90 translate<1.3,2,0>} texture {T_Grnt1 scale 1} finish{phong 1 reflection 0.2} } //----------------ground disc{0, <0,0,1>, 12 pigment{brick White, CoolCopper*0.7 scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ prism の構文 ＞

prism { [ linear_sweep | conic_sweep ] [ linear_spline | quadratic_spline | cubic_spline | bezier_spline ] HEIGHT1, HEIGHT2, TOTAL_NUMBER_OF_POINTS, <POINT_1>, <POINT_2>, ..., <POINT_n> [ open ] [ sturm ] [ OBJECT_MODIFIERS... ] }
prism 角柱のキーワード
linear_sweep 直線スイープ、スイープの間、要素図形のサイズは変わらない。[デフォルト：linear_sweep ]
conic_sweep 円錐スイープ、スイープの間、要素図形のサイズを縮小していき、角錐状の物体を作る。 ▷ 円錐（角錐）スイープ 参照
linear_spline ２次元図形に対する１次スプラインの設定、各点は直線で結ばれる。[デフォルト：linear_spline ]
quadratic_spline ２次元図形に対する２次スプラインの設定、曲線の始まりの傾きを制御できる。
cubic_spline ２次元図形に対する３次スプラインの設定、曲線の始まりと終わりの傾きを制御できる。
bezier_spline ２次元図形に対するbezierスプラインの設定
HEIGHT1 スイープの始点のy座標、角柱の底部の高さ
HEIGHT2 スイープの終点のy座標、角柱の頂部の高さ
TOTAL_NUMBER_OF_POINTS スプラインに使用する点の総数
<POINT_1>～<POINT_n> スプラインに使用する各点の x,z 座標
open 角柱の両端面を取り除く設定
sturm 形状が正しく描かれない場合に、時間をかけて正確に計算をする設定（３次スプラインのみ）
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

※ open を使用した角柱は CSG では適切に描かれない場合がある。 ※ スプライン：▷「11.1-14 回転体：スプライン曲線について」参照

● prism の２次元図形設定
１つの prism に２次元図形が複数設定できる。図形が重なりあわなければ、それらの図形はそのままスイープされ複数立体が生成される。２次元図形が重なりあった場合には、重なった部分は空洞となる。次の図はそのような重なりあった場合の例である。

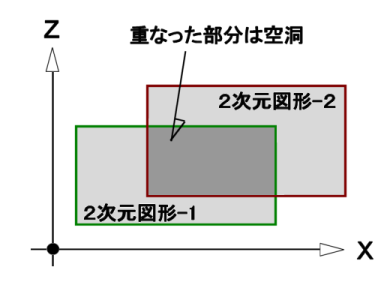図11.1-16b　重なる２次元図形

次の 図11.1-16c は、１つの prism の中に３つの図形を定義したものである。左側は 上図のような２つの重なりあう四角形と重ならない四角形の３つを定義し、linear_splineのスイープを使った。右側は同じ３つの図形を用いて、quadratic_splineでスイープを行った例である。

図11.1-16c　３つの２次元図形からなる prism
//--------------- Fig. 11.1-16c /prism/ #version 3.7 #include "colors.inc" #include "textures.inc" #include "Woods.inc" global_settings {assumed_gamma 2.2} camera{ location<5,-20,9.5> sky<0,0,1> right <-image_width/image_height,0,0> look_at<-0.4,0,1.4> angle 18 } light_source {<500,-500,1000> color White*1.5} //=================================== prism define (sweep rectangle) #declare prism_2a= prism{ linear_sweep linear_spline 0,3.5, 15 <0,0>,<1.5,0>,<1.5,1>,<0,1>,<0,0>, //--onject 1 <0.5,0.5>,<2,0.5>,<2,1.5>,<0.5,1.5>,<0.5,0.5> //--onject 2 <0.5,2>,<2,2>,<2,2.5>,<0.5,2.5>,<0.5,2> //--onject 3 } #declare prism_2b= prism{ linear_sweep quadratic_spline 0,3.5, 18 <0,0>,<1.5,0>,<1.5,1>,<0,1>,<0,0>,<1.5,0>, //--onject 1 <0.5,0.5>,<2,0.5>,<2,1.5>,<0.5,1.5>, //--onject 2 <0.5,0.5>,<2,0.5> <0.5,2>,<2,2>,<2,2.5>,<0.5,2.5>,<0.5,2>,<2,2> //--onject 3 } //=================================== /// prism Object /// union{ object{prism_2a translate<-2.5,-3,1>} texture {Yellow_Pine} finish{phong 1 reflection 0.2} } union{ object{prism_2b translate<0.5,-3,1>} texture {T_Wood7 scale 0.8} finish{phong 1 reflection 0.2} } //----------------ground disc{0, <0,0,1>, 12 pigment{brick White, CoolCopper*0.7 scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

● 円錐スイープ
円錐スイープでは 原点 <0,0,0> が頂点となり、±y 方向にサイズが大きくなっていく。y=1 の位置に置いた x-z 平面の２次元図形と原点でできる円錐（角錐）が生成される。この形状を、HEIGHT1 と HEIGHT2 で設定した高さ y 値で切り取られる。円錐や角錐を作成するときは、HEIGHT1 または HEIGHT2 のどちらかに 0 を設定する。これらの位置関係を 下図11.1-16d に示す。

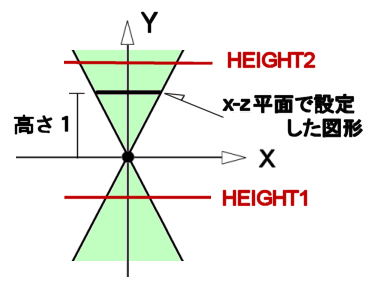図11.1-16d　円錐スイープ

図11.1-16e　角錐（conic_sweep）

上図は、同じ２次元図形を conic_sweep して角錐を生成している。切り出す HEIGHT1 と HEIGHT2 の違いで、このような図形の差がでている。

//--------------- Fig. 11.1-16e /prism/ #version 3.7 #include "colors.inc" #include "textures.inc" #include "stones.inc" global_settings {assumed_gamma 2.2} camera{ location<5,-20,9> sky<0,0,1> right <-image_width/image_height,0,0> look_at<-0.3,0,1.3> angle 22 } light_source {<200,-500,1000> color White*1.5} //=============================== /// conic_sweep /// prism{ conic_sweep linear_spline -2,2, 5, <-0.5,-0.3>,<0.5,-0.3>,<0.5,0.3>,<-0.5,0.3>,<-0.5,-0.3> rotate x*90 translate<-2,-2,2> texture {T_Grnt9 scale 0.3} } prism{ conic_sweep linear_spline -4,0, 5, <-0.5,-0.3>,<0.5,-0.3>,<0.5,0.3>,<-0.5,0.3>,<-0.5,-0.3> rotate x*90 translate<1.5,-1,4> texture {T_Grnt9 scale 0.3} } //----------------ground disc{0, <0,0,1>, 12 pigment{brick White, CoolCopper*0.7 scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

11.1-17　球スイープ（sphere_sweep）

球体が移動したときの軌跡によりできる立体である。球の移動点を設定するとスイープ図形が生成される。

図11.1-17　球スイープ（sphere_sweep）
//--------------- Fig. 11.1-17 sphere_sweep #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-10,5> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0.3> angle 20 } light_source {<0,-5,5> color 1.5 parallel point_at <5,-1,0>} //======================== /// sphere_sweep /// sphere_sweep { linear_spline, 4, <-0.5,0,0>, 0.1 <-0.5,0,1>, 0.1 < 0.5,0,0>, 0.1 < 0.5,0,1>, 0.1 pigment{color rgb<0.8,0.75,0.65>*1.5} finish{phong 1 specular 0.3} } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} translate z*-0.2 } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：△（マージ×）

＜ sphere_sweep の構文 ＞

sphere_sweep { [ linear_spline | b_spline | cubic_spline ] NUM_OF_SPHERES, <CENTER>, RADIUS <CENTER>, RADIUS ... <CENTER>, RADIUS [ tolerance DEPTH_TOLERANCE ] [ OBJECT_MODIFIERS... ] }
sphere_sweep 球スイープのキーワード
linear_spline １次スプラインの設定。各点は直線で結ばれる。
b_spline B-スプラインの設定
cubic_spline ３次スプラインの設定。曲線の始まりと終わりの傾きを制御できる。
NUM_OF_SPHERES 点数
<CENTER> 球の中心の x,y,z 座標
RADIUS 球の半径
tolerance DEPTH_TOLERANCE 許容誤差の設定　[デフォルト：10.e-6 ]
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

※ 許容誤差 ： レイトレーシングで影の判定を行うときに、判定点において光源の方向に物体が存在するかどうかを調べる。物体が存在するとその物体までの距離が計算される。許容誤差とはこの距離の最小値を指し、これ以上の値を影であると判定する。許容誤差が小さすぎると球スイープ物体自身が影の物体と判定され、黒い点のようなものが発生することがある。このような場合は、許容誤差を大きくする。

　▷ 次を見る