▷ 前を見る　

11.1-18　ハイトフィールド（height_field）

ハイトフィールドは非常に多くの小さな３角形によって凹凸のある面を表現するものである。凹凸の形状は濃淡画像（またはパレットインデックス）を高さに変換して生成される。Paint Shopなどの画像ソフトを使って、地形図を等高線で色分けして実際の地形を表現するといった使い方もできる。

図11.1-18a　ハイトフィールド

上図の山々のような図形は、下の 図11.1-18b のモノクロ画像から生成している。

//--------------- Fig. 11.1-18a /height_field/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<3,-3,1> sky<0,0,1> right <-image_width/image_height,0,0> look_at<1,-1,0.05> angle 45 } light_source {<300,-500,500> color White*1.2} //======================= /// height_field /// height_field{ png "prz-111-18b-hf-image.png" smooth rotate x*90 scale<2,2,0.6> pigment{color rgb<0.8,0.6,0.4>*0.7} translate z*0.01 } //--------------------------------ground disc{0, <0,0,1>, 5 pigment{color Wheat*1.5} } //--------------------------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ height_field の構文 ＞

height_field { FILE_TYPE "FILE_NAME" [ smooth ] [ hierarchy on|off] [ water_level FLOAT ] [ OBJECT_MODIFIERS... ] }
height_field ハイトフィールドのキーワード
FILE_TYPE 画像のファイル形式を次の中から設定する。
　gif、tga、pot、png、pgm、ppm、jpeg、tiff、SYS
※SYSは使用するプラットフォーム固有の形式
FILE_NAME 画像のファイル名の設定、カレントディレクトリとLibrary_pathを設定したディレクトリ以外の場所にあるファイルは、次のようにフルパスで設定しなければならない。例）DドライブのpovfileディレクトリにあるImage.gifファイルを設定する場合
height_field { gif " d:\povfile\Image.gif "
smooth ３角形で構成されいる表面を滑らかにする設定
hierarchy　on|off 階層バウンディングのスイッチ　[ディフォルト：on]
water_level FLOAT 設定した高さ以下の部分をカットする。[ディフォルト：0 ]
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

図11.1-18b　ハイトフィールド生成用の画像

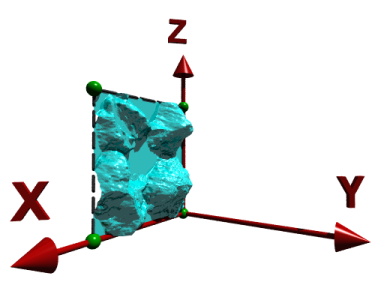図11.1-18c　ハイトフィールドの向きと大きさ

ハイトフィールドは次のようにして生成される。

　(1)画像を x-z 平面に1x1の大きさ で投影する。
 　(2)濃淡を 0～1 の高さデータに変換する。白（rgb 1）がもっとも高く、黒（rgb 0）がもっとも低くなる。
 　(3)変換した高さデータをもとに、画像を +y 方向に隆起させる。

※ 図11.1-8b の画像を使ってにハイトフィールドを作ると、右手座標系では 図11.1-8c のよう生成されるので、X 軸回りに+90度の回転を行う。

ハイトフィールドの滑らかさは、使用する画像のフォーマットと解像度に依存する。

●平面方向（x-z方向）の滑らかさは使用する画像の解像度に依存する。もとの 画像の解像度が大きくなると、ハイトフィールドを生成する３角形の分割数が多くなり、 結果として平面方向でより滑らかになる。

●高さ方向（y方向）の滑らかさは使用する画像ファイル形式に依存する。画像ファイ ルは形式によって使用できる色数が異なる。ハイトフィールドは色の濃淡かパレット インデックスをもとに高さを計算するため、使用できる色が多いほど高さ方向の分割 数が多くなり、結果として高さ方向でより滑らかになる。例えばgif形式の画像は使用 できる色数が256色であるため高さは256段階になるが、tga画像では65536色使用で きるため、高さは65536段階になる。

＜ハイトフィールドで使用できる画像ファイル形式＞

gif 256色（8ビット）のファイル形式であり、高さデータとしてカラーパレットを使用する。パレットインデックス0が高さ0になり、255が高さ1になる。
tga 赤と緑のプレーンが高さ変換に使用される。赤が上位バイトで緑が下位バイトとなり、65536段階（16ビット）の高さに変換される。
pot 16ビット（65536色）のパレットを持っており、65536段階の高さに変換される。
png グレースケール16ビット（65536色）形式のPGN画像が変換に使用される。
pgm pnm形式のグレースケール画像ファイルで、65536段階（16ビット）の高さに変換される。
ppm pnm形式のカラー画像ファイルで、65536段階（16ビット）の高さに変換される。tgaファイルと同様な変換をする。
jpeg デジカメなどでよく使用されている圧縮カラー画像ファイルで、圧縮率が高いと画像が劣化する。
tiff さまざまなオプションのある画像フォーマットである。
SYS Windowsのbmp、Macintoshのpictなど、プラットフォーム標準の形式。

※ POV-Rayでレンダリングした画像はtga形式などで特定のディレクトリに出力されるので、 POV-Rayのシーンのイメージをそのまま使うこともできる。また、その特定のディレクト リにLibrary_Pathを設定しておけば " シーンファイル名.tga " と設定するだけでそのシ ーンのイメージをハイトフィールドに使うことができる。

オプションの water_level を設定し、任意の高さより下の部分をカットできる。ハイトフィールドとして不要な部分を切り捨てたい場合に便利である（もとの画像の背景色が平面になって現れた場合など：図11.1.8d参照）。

ハイトフィールドは多くの平らな３角形でできているため、表面が角張って見えることがある。このような場合、オプションのsmoothを設定するこで、３角形のつなぎ目を（見かけ上）滑らかにできる。

図11.1-18d　water_levelを設定した場合（右側）
//--------------- Fig. 11.1-18d /height_field/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-4.1,10> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,-0.1,0> angle 14 } light_source {<0,-500,800> color White*1.2} //========================== /// height_field /// height_field{ png "prz-111-18b-hf-image.png" smooth rotate x*90 scale <1,1,0.3> pigment{color rgb<0.8,0.6,0.4>*0.8} translate <-1.1,0,0.8> } height_field{ png "prz-111-18b-hf-image.png" smooth water_level 0.01 //<<<-----------water_level rotate x*90 scale <1,1,0.3> pigment{color rgb<0.8,0.6,0.4>*0.7} translate <0.1,0,0.8> } //--------------------------------ground disc{0, <0,0,1>, 5 pigment{color Wheat*1.5} }

これまでの例で示したハイトフィールドを使って、水面を表現した例を次の図11.1-18eに示す。

図11.1-18e　水面を追加したハイトフィールド
//--------------- Fig. 11.1-18e /height_field/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<3,-3,1> sky<0,0,1> right <-image_width/image_height,0,0> look_at<1,-1,0.05> angle 38 } //light_source {<300,-500,1000> color White} light_source {<300,-500,500> color White} //============================ /// height_field /// height_field{ png "prz-111-18b-hf-image.png" smooth water_level 0.17 //-----water_level rotate x*90 scale<2,2,0.6> pigment{color rgb<0.8,0.6,0.4>*0.7} // translate z*0.01 } //--------------------------------water disc{0, <0,0,1>, 20 pigment{color rgbf<0.3,0.6,1,0.7>} normal{wrinkles 1 scale 0.2} finish{reflection 0.5} translate<0,0,0.11> } //--------------------------------ground disc{0, <0,0,1>, 20 pigment{color Wheat} } //--------------------------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

11.1-19　ブロブ（blob）

ブロブは球や円柱を融合したような形状を生成することができる。このような融合は図形の中心か発する電界の等しい点の集合として考案された。全体の境界値と各要素図形の電界の強さが等しくなる部分が表面として現れ、結果として球や円柱が融合したような図形が生成される。

図11.1-19a　ブロブ

円柱１つと球が２つ融合（滑らかに結合）しているブロブである。融合の程度は threshold 値でコントロールできる。

//--------------- Fig. 11.1-19a /blob/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<1,-3,2> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,1> } light_source {<300,-500,1000> color White} //=============================== /// blob /// blob{ threshold 0.27 sphere{<-1,0,3>,1.5, strength 0.5} sphere{<1,0,3>,1.5, strength 0.5} cylinder{-x*2,x*2,1.5, strength 0.5 translate z*1} pigment{color rgb<1,0.8,0.3>*1.5} finish{phong 1 reflection 0.1} scale 0.5 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ blob の構文 ＞

blob { threshold FLOAT sphere { <CENTER>, RADIUS_s, [ strength ] STRENGTH_s [ OBJECT_MODIFIERS... ] } cylinder { <END1>, <END2>, RADIUS_c, [ strength ] STRENGTH_c [ OBJECT_MODIFIERS... ] } [ hierarchy on|off ] [ sturm ] [ OBJECT_MODIFIERS... ] }
blob ブロブのキーワード
threshold FLOAT 全体の境界値（0以上の値）：下記を参照 [デフォルト：1 ]
sphere 球のキーワード ▷「11.1-2 球」参照
<CENTER> 球の中心 x,y,z 座標
RADIUS_s 球の半径、scaleを使用すれば楕円球などになる。
strength 球の中心の強さキーワード：省略可
STRENGTH_s 球の中心の強さ：下記 STRENGTH 参照
cylinder 円柱のキーワード ▷「11.1-3 円柱」参照
<END1>, <END2> 円柱の両端の中心 x,y,z 座標
RADIUS_c 円柱の半径
strength 円柱の中心の強さキーワード：省略可
STRENGTH_c 円柱の中心の強さ：下記 STRENGTH 参照
hierarchy on|off 階層バウンディングのスイッチ　[デフォルト：on]
sturm 形状が正しく描かれない場合に、時間をかけて正確に計算をする設定
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

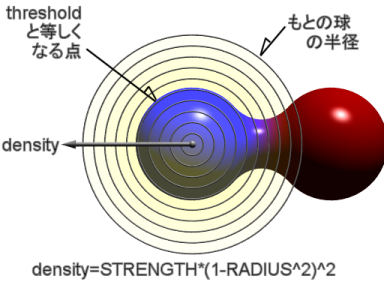図11.1-19b　ブロブのパラメータの関係

threshold と density の値が等しくなる点に面が生成される。

※ threshold について
・threshold ＞ 0 に設定する。
・threshold を大きくすると、現れる表面はその物体の中心に近くなる。
・threshold を小さくすると、現れる表面はその物体の本来の表面に近くなる。

※ STRENGTH について
・STRENGTH ＞ 0 で、その値が threshold の値よりも大きければその物体は見える。
・STRENGTH ＝ 0 のときはその物体は見えない。
・STRENGTH ＜ 0 のときもその物体は見えないが、その物体の近くにある物体はこの負の値の影響によって削られる。

11.1-20　フラクタル（julia_fractal）

フラクタルは、４次元のパラメータを設定によって、何かをねじったような不思議な形状を生成できる。

図11.1-20 フラクタル
//--------------- Fig. 11.1-20 /julia_fractal/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<2,-2,2> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,1> } light_source {<300,-500,1000> color White} //======================== /// julia_fractal /// julia_fractal { <0.3,0.5,0.0,0.3> quaternion pigment{color rgb<1,0.6,0>*1.5} finish{phong 1} rotate <0,-90,180> translate z*1 } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.3 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ julia_fractal の構文 ＞

julia_fractal { 4DJULIA_PARAMETER [ quaternion | hypercomplex ] [ sqr | cube | exp | reciprocal | sin | asin | sinh | asinh | cos | acos | cosh | acosh | tan | atan | tanh | atanh | ln | log | pwr(X,Y) ] [ max_iteration MAX_ITERATION ] [ precision PRECISION ] [ slice 4DNORMAL, DISTANCE ] }
julia_fractal フラクタルのキーワード
4D JULIA_PARAMETER ジュリア集合の４次元パラメータ　[デフォルト：<1,0,0,0> ]
quaternion、hypercomplex フラクタルの計算に使用する方程式の設定 [デフォルト：quaternion ]
sqr、 ... 、pwr(X,Y) 関数の設定 [デフォルト： sqr ]
max_iteration MAX_ITERATION 　[デフォルト：20 ]
precision PRECISION 　[デフォルト：20 ]
slice 4DNORMAL, DISTANCE 　[デフォルト：<0,0,0,1>,0 ]

11.1-21　3Dテキスト（text）

ttf（True Type font）フォントの文字を３次元物体として生成することができる。

図11.1-21a　3Dテキスト

上図11.1-21a は、POV-Rayに添付されているフォントから文字を３D形状に生成したものである。

//--------------- Fig. 11.1-21a /text/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-4.5,1.5> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,1.2> angle 80 } light_source {<300,-1000,1000> color White} //====================================== /// 3D text 1 /// text{ttf "timrom.ttf","POV-Ray",1,x*-0.03 scale <1,1,0.3> pigment{Yellow*1.3} finish{phong 1 reflection 0.3} rotate x*90 translate <-2,-1.5,0.25> } //====================================== /// 3D text 2 /// text{ttf "cyrvetic.ttf","POV-Ray",1,x*-0.03 scale <1,1,0.2> pigment{Cyan*1.5} finish{phong 1 reflection 0.3} rotate x*90 translate <-1.8,-1.5,1.2> } //====================================== /// 3D text 3 /// text{ttf "cyrvetic.ttf","POV-Ray",1,x*-0.03 scale <1,1.5,0.5> pigment{Green*1.5} finish{phong 1 reflection 0.3} rotate x*90 translate <-2,1,2.8> } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.1 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限ソリッド
　　●クリッピング形状：○
　　●CSG：○

＜ text の構文 ＞

text { ttf " FONTNAME.TTF " , " STRING_OF_TEXT " , THICKNESS_FLOAT , OFFSET_VECTOR [ OBJECT_MODIFIERS... ] }
text 3Dテキストのキーワード
ttf " FONTNAME.TTF" フォントファイル名（字体）の設定、ttf（True Type font）しか使用できない。POv-Ray 添付のフォントは３種類ある。
crystal.ttf　　等幅フォント
cyrvetic.ttf　 プロポーショナル
timrom.ttf　　プロポーショナル
" STRING_OF_TEXT " 文字列表現（印刷可能な文字しか使用できない。）文字列表現の詳細は「1.6 文字列」を参照
THICKNESS_FLOAT 3Dテキストの厚さの設定
OFFSET_VECTOR 文字の x,y 方向の間隔の設定。たとえば0.1*xと設定すると、文字の x 方向の間隔が 0.1 になる。通常は0を設定する。
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

※ 通常、文字の高さは0.5～0.75程度になる。

3Dテキストは、最初の文字の手前左下を原点として x-y 平面上に描かれ、+z 方向が文字の厚みになる。（下図11.1-21b参照）。x 軸回りに +90 度回転すると 文字が立った状態になる。

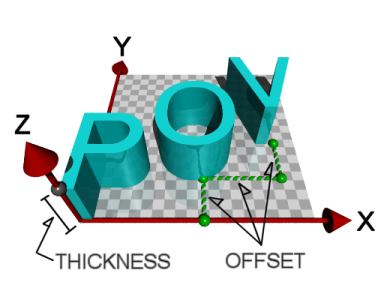図11.1-21b　3Dテキストの位置、向き、パラメータの関係

11.1-22　無限平面（plane）

面の放線ベクトルと原点からの距離を設定するだけで無限平面を簡単に設定できる。また、大きさが無限であるため空間を完全に内側と外側に分ける（法線ベクトル方向が外側）と定義されており、CSGで使うこともできる。

図11.1-22　無限平面
//--------------- Fig. 11.1-22 /plane/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-1,0.35> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0> } light_source {<-30,-50,100> color White} //============================== /// plane /// plane{z,0 pigment{checker White*1.2, color rgb<0.5,0.9,0.9>*0.5 scale 0.2} finish{phong 1 reflection 0.3} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：無限パッチ
　　●クリッピング形状：○
　　●CSG：○

＜ plane の構文 ＞

plane { <NORMAL>, DISTANCE [ OBJECT_MODIFIERS... ] }
plane 無限平面のキーワード
<NORMAL> 面の法線ベクトル、平面の向きと、空間の内側、外側を決定する。
DISTANCE 法線ベクトル方向の原点と平面の距離
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

法線ベクトルは通常は組み込み識別子 x、y、z を使って設定する。例えば、plane { z, 0 }は、plane { <0, 0, 1>, 0 }と同じ意味である。

11.1-23　２次曲面（quadric）

２次方程式の各項の係数を設定し２次曲面を作ることができる。２次曲面には、楕円体、球、コーン、円柱、放物面、双曲面などがある。

（上）楕円面、 １葉双曲面、 ２葉双曲面
（中）楕円錐面、楕円放物面、双曲放物面
（下）楕円柱面、　放物柱面、　双曲柱面
図11.1-23　２次曲面
//--------------- Fig. 11.1-23 /quadric/ #version 3.7 #include "colors.inc" #include "textures.inc" global_settings {assumed_gamma 2.2} #default{ //-----------------texture declare pigment{checker SlateBlue, White*.8 scale 0.4} finish{phong 1 reflection 0.1} } camera{ location<0,-40,0.01> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0> angle 15 } light_source {<-100,-1000,-100> color White*1} light_source {<100,-1000,-100> color White*1} //================================== up ==== /// quadric-1 /// quadric{<0.5,1,1>,<0,0,0>,<0,0,0>,-1 scale 0.8 translate<-3,1,2.5> } quadric{<1,1,-1>,<0,0,0>,<0,0,0>,-1 clipped_by{box{-5,5}} scale 0.2 rotate x*30 translate<0,1,2> } quadric{<-1,-1,1>,<0,0,0>,<0,0,0>,-1 clipped_by{box{-5,5}} scale 0.2 rotate x*30 translate<3,1,2> } //================================= middle === /// quadric-2 /// quadric{<1,1,-1>,<0,0,0>,<0,0,0>,0 clipped_by{box{-5,5}} scale 0.2 rotate x*30 translate<-3,0,0> } quadric{<1,1,0>,<0,0,0>,<0,0,1>,0 clipped_by{box{-5,5} translate z*-5} scale 0.2 rotate x*30 translate<0,0,0.5> } quadric{<1,-0.5,0>,<0,0,0>,<0,0,1>,0 clipped_by{box{-5,5}} scale 0.2 rotate z*90 rotate x*30 translate<3,0,-0.5> } //================================== down === /// quadric-3 /// quadric{<0.3,1,0>,<0,0,0>,<0,0,0>,-0.5 clipped_by{box{-5,5}} scale z*0.2 rotate x*60 translate<-3,-1,-2.5> } quadric{<1,-1,0>,<0,0,0>,<0,0,0>,-1 clipped_by{box{-5,5}} scale 0.2 rotate x*60 translate<0,-1,-2.5> } quadric{<0,0.5,0>,<0,0,0>,<1,0,0>,0 clipped_by{box{-5,5}} scale 0.2 rotate z*90 rotate x*60 translate<3,-1,-2.5> } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：無限パッチ
　　●クリッピング形状：○
　　●CSG：○

＜ quadric の構文 ＞

quadric { <A,B,C>, <D,E,F>, <G,H,I>, J [ OBJECT_MODIFIERS... ] }
quadric ２次曲面のキーワード
A～ J 下記の２次方程式の各項の係数
＜２次曲面の方程式＞
Ax^2 + By^2 + Cz^2 +
Dxy + Exz + Fyz +
Gx + Hy + Iz + J = 0
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

インクルードファイルshapesq.incに高次曲面による形状がいくつか定義されている。また、POVRAY\Povscn\Mathの中にそれらを用いたデモシーンがあるのでそれらを参照する。

11.1-24　３次曲面（cubic）

３次方程式の各項の係数を与えることで曲面が生成される。このためどのような３次曲面でも作成可能であるが、思うような曲面の係数を求めることは煩雑である。

図11.1-24　３次曲面
//--------------- Fig. 11.1-24 /cubic/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<10,-10,2> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0> } light_source {<300,-500,1000> color White parallel point_at 0 } //=============================== /// cubic /// cubic{<1,0,0,0,0, 0,1,0,0,0, 0,0,1,0,0, 0,0,0,6,0> sturm pigment{checker White*1.2, Green scale 2} finish{phong 1 reflection 0.1} rotate <0,-90,90> } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：無限パッチ
　　●クリッピング形状：○
　　●CSG：○

＜ cubic の構文 ＞

cubic { <T1, T2,... T20> [ sturm ] [ OBJECT_MODIFIERS... ] }
cubic ３次曲面のキーワード
<T1, T2, ..., T20> ３次方程式の各項の係数。
sturm 形状が正しく描かれない場合に、時間をかけて正確に計算をする設定
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

インクルードファイルshapesq.incに高次曲面による形状がいくつか定義されている。また、POVRAY\Povscn\Mathの中にそれらを用いたデモシーンがあるのでそれらを参照する。

11.1-25　４次曲面（quartic）

４次方程式の各項の係数を設定し４次曲面を作ることができる。

図11.1-25　4次曲面
//--------------- Fig. 11.1-25 /quartic/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-10,10> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0> } light_source {<1000,-1000,1000> color White} //============================ /// quartic /// quartic{ <1,0,0,0,0,0,0, 0,1,0,0,0,0,0, 0,0,1,0,0,0,0, 0,0,0,1,0,0,0, 0,0,0,0,1,0,1> pigment{checker White*1.2, Red} finish{phong 1 reflection 0.2} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：無限パッチ
　　●クリッピング形状：○
　　●CSG：○

＜ quartic の構文 ＞

quartic { <T1, T2,... T35> [ sturm ] [ OBJECT_MODIFIERS... ] }
quartic ４次曲面のキーワード
<T1, T2,... T35> ４次方程式の係数
sturm 形状が正しく描かれない場合に、時間をかけて正確に計算をする設定
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

インクルードファイルshapesq.incに４次曲面による形状がいくつか定義されている。また、POVRAY\Povscn\Mathの中にそれらを用いたデモシーンがあるのでそれらを参照する。

11.1-26　高次曲面（poly）

２～７次方程式の各項の係数を設定し、複雑な高次曲面を作ることができる。

図11.1-26　高次曲面
//--------------- Fig. 11.1-26 /poly/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<0,-10,10> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0> } light_source {<0,1000,10000> color White} //=========================== /// poly /// poly{ 5, <1,0,0,0,0,0,0,0, 0,1,0,0,0,0,0,0, 0,0,1,0,0,0,0,0, 0,0,0,1,0,0,0,0, 0,0,0,0,1,0,0,0, 0,0,0,0,0,1,0,0, 0,0,0,0,0,0,1,1> pigment{checker White*1.2, Yellow} finish{phong 1 reflection 0.1} rotate y*-90 } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：無限パッチ
　　●クリッピング形状：○
　　●CSG：○

＜ poly の構文 ＞

poly { ORDER, <T1, T2, T3, .... Tm> [ sturm ] [ OBJECT_MODIFIERS... ] }
poly 高次曲面のキーワード
ORDER 曲面の方程式の次数（2～7 の整数）
<T1, T2, ..., Tm> ２～７次方程式の各項の係数
※ m = ((ORDER+1)*(ORDER+2)*(ORDER+3))/6
sturm 形状が正しく描かれない場合に、時間をかけて正確に計算をする設定
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

インクルードファイルshapesq.incに高次曲面（poly）による形状がいくつか定義されている。

11.1-27　ベジエ曲面（bicubic_patch）

ベジエ曲面は16個の制御点によって平面形状を決定する３次元曲面である（図11.1-26b参照）。複雑な屋根などの形状を表現できる。

図11.1-27a　ベジエ曲面
//--------------- Fig. 11.1-27a /bicubic_patch/ #version 3.7 #include "colors.inc" global_settings {assumed_gamma 2.2} camera{ location<1,-4,1> sky<0,0,1> right <-image_width/image_height,0,0> look_at<0,0,0.5> } light_source {<0,1000,1000> color White} //========================== /// bicubic_patch /// bicubic_patch{ type 1 flatness 0 u_steps 4 v_steps 4 <0,0,0>,<1,0,1>,<2,0,1>,<3,0,0> <0,1,1>,<1,1,1>,<2,1,1>,<3,1,1> <0,2,1>,<1,2,1>,<2,2,1>,<3,2,1> <0,3,0>,<1,3,1>,<2,3,1>,<3,3,2> pigment{checker White*1.2, BrightGold scale 0.5} finish{phong 1 reflection 0.2} translate <-1.5,-1.5,0> } //----------------ground disc{0, <0,0,1>, 5 pigment{brick White, CoolCopper scale 0.08} normal{brick 0.01 scale 0.1} finish{reflection 0.1 crand 0.1} } //----------------sky sky_sphere{ pigment{ wrinkles color_map{ [ 0.4 SkyBlue] [ 0.9 White ] } scale <1, 0.2, 0.2> } }

　　●プリミティブのタイプ：有限パッチ
　　●クリッピング形状：○
　　●CSG：△（曲面の端部は×）

＜ bicubic_patch の構文 ＞

bicubic_patch { type 0 | 1 flatness FLOAT u_steps INTEGE v_steps INTEGER <CP1>, <CP2>, <CP3>, <CP4>, <CP5>, <CP6>, <CP7>, <CP8>, <CP9>, <CP10>, <CP11>, <CP12>, <CP13>, <CP14>, <CP15>, <CP16> [ OBJECT_MODIFIERS... ] }
bicubic_patch ベジエ曲面のキーワード
type 0 | 1 ベジエ曲面のタイプの設定。
●type 0：メモリ消費が少ないがレンダリングは遅い。
●type 1：メモリ消費が多いがレンダリングは速い。
flatness FLOAT 曲面の滑らかさを0～1で設定する。値を大きくすると曲率
の大きい部分ほど滑らかになり、そうでない部分は簡易的に描
かれる。flatness 0で全体が平均的に滑らかになる。
※ 値を大きくし過ぎると、曲面上に亀裂が生じる場合がある。
u_steps INTEGER 曲面を縦方向に分割する３角形の数の最小値（通常 4 以下）
v_steps INTEGER 曲面を横方向に分割する３角形の数の最小値（通常 4 以下）
<CP1> ～ <CP16> 曲面の制御点の x,y,z 座標（図11.1-26b参照）
OBJECT_MODIFIERS... 物体の変形・テクスチャなどの設定

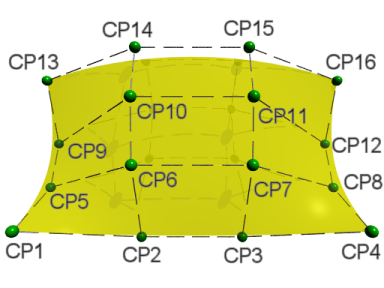図11.1-27b　ベジエ曲面の制御点

　▷ 次を見る